揭秘：sec x 的倒数，究竟是 sin x 还是另有其“人”？

在数学领域中，关于三角函数的性质、关系及其倒数的问题一直备受关注。其中，“sec x的倒数是sin x还是cos x?”这一问题尤为常见，它涉及到了三角函数的基本概念及其相互之间的关系。为了深入探讨这一问题，我们需要从三角函数的定义出发，逐步推导并理解各个三角函数之间的倒数关系。

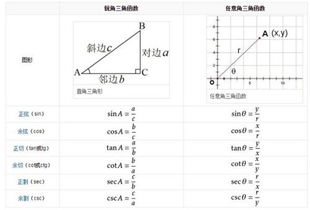
三角函数，作为描述直角三角形中边长比例的数学工具，在几何学和物理学等领域有着广泛的应用。其中，sec x（正割函数）是余弦函数的倒数，即sec x = 1/cos x。而sin x（正弦函数）和cos x（余弦函数）则是描述直角三角形中锐角对应的对边与斜边之比、邻边与斜边之比的函数。在探讨sec x的倒数时，我们首先要明确的是，一个函数的倒数是指该函数值与其乘积为1的另一个函数。

根据三角函数的定义，我们可以知道，sec x与cos x互为倒数，即sec x * cos x = 1。由此，我们可以推断出sec x的倒数是cos x，而不是sin x。这一点是理解三角函数倒数关系的关键所在。

为了更深入地理解这一关系，我们可以从三角函数的图像和性质出发进行分析。在三角函数的图像中，sec x的图像与cos x的图像在形状上有所不同，但它们的倒数关系在图像上也有所体现。例如，在sec x的图像中，当cos x的值接近0时（即角度接近π/2的奇数倍时），sec x的值会趋于无穷大。这是因为此时cos x作为分母接近0，而sec x作为倒数则相应地趋于无穷大。这一现象从另一个角度验证了sec x与cos x之间的倒数关系。

此外，我们还可以从三角函数的周期性出发进行分析。正弦函数sin x和余弦函数cos x都是周期函数，它们的周期为2π。而正割函数sec x作为余弦函数的倒数，也具有周期性，但其周期与cos x不同。这是因为当cos x的值在周期内的某个区间内为负数时，sec x的值也会相应地变为负数。然而，这并不影响sec x与cos x之间的倒数关系。在任何周期内，只要cos x的值不为0（因为0没有倒数），sec x的值就始终为1除以cos x的值。

在理解了sec x与cos x之间的倒数关系后，我们再来看看sin x在其中的位置。正弦函数sin x与余弦函数cos x之间有着密切的关系，它们之间满足Pythagorean identity（毕达哥拉斯恒等式）：sin²x + cos²x = 1。这个恒等式揭示了正弦函数和余弦函数之间的平方和关系，但并未直接涉及它们的倒数关系。因此，在探讨sec x的倒数时，我们不能将sin x与cos x混为一谈。

为了进一步巩固对sec x倒数关系的理解，我们可以尝试通过一些具体的例子进行验证。例如，当x = π/4时（即45°角），我们知道cos x = √2/2，sin x = √2/2。此时，sec x = 1/cos x = √2/（√2/2） = 2。而sec x的倒数为1/2，这与cos x = √2/2（也等于1/2的倒数）是一致的。这个例子再次验证了sec x的倒数是cos x的结论。

除了通过具体的例子进行验证外，我们还可以利用三角函数的诱导公式和同角三角函数的基本关系进行推导。诱导公式可以帮助我们将角度转换到已知的范围内进行计算；而同角三角函数的基本关系则揭示了正弦、余弦、正切等函数之间的内在联系。通过这些公式的推导和应用，我们可以更加深入地理解三角函数之间的倒数关系以及它们之间的其他性质。

综上所述，sec x的倒数是cos x而不是sin x。这一结论是基于三角函数的定义、图像、性质以及诱导公式和同角三角函数的基本关系得出的。在理解和应用这一结论时，我们需要注意区分不同三角函数之间的关系以及它们在不同条件下的取值范围。只有这样，我们才能更加准确地运用三角函数来解决实际问题并提高我们的数学素养。

此外，值得一提的是，虽然sec x的倒数是cos x这一结论在数学上是确定的，但在实际应用中我们还需要根据具体问题的背景和条件进行灵活分析和处理。例如，在某些物理或工程问题中，我们可能需要考虑角度的取值范围、三角函数的正负性以及它们之间的比值关系等因素来求解问题。因此，在学习和应用三角函数时，我们需要保持开放和灵活的思维态度，不断探索和实践新的方法和技巧来解决问题。