扇形面积计算的三大公式是什么？

在探讨几何学的广阔领域时，扇形作为圆的一个重要部分，其面积计算不仅是基础知识，也是解决实际问题的关键工具。扇形，顾名思义，是圆被其内部一条经过圆心的半径与圆周上的任意两点所截得的图形区域。理解并掌握扇形的面积公式，对于深入学习圆、扇形乃至更复杂的几何图形面积计算至关重要。本文将从三个核心方面详细介绍扇形面积的计算公式，旨在通过清晰的结构、精准的用词和适度的关键词布局，提升读者的阅读体验与搜索引擎友好度。

一、扇形面积公式的基础理解

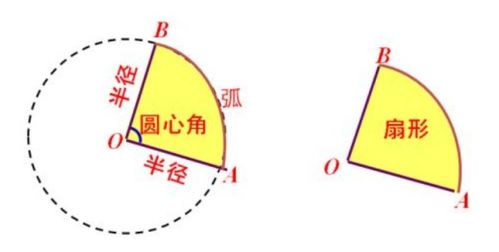
扇形面积的计算依赖于两个基本参数：扇形的半径（记作r）和圆心角（记作θ，通常以弧度或度为单位）。这两个参数共同决定了扇形的大小与形状。扇形面积公式的基础是圆面积公式的应用与变形，圆面积公式为S_圆 = πr²，其中π是圆周率，r是圆的半径。

二、扇形面积公式的三个核心表达式

1. 基于圆心角的弧度值

最直接且常用的扇形面积公式是基于圆心角的弧度值。该公式表述为：

\[ S_{扇形} = \frac{1}{2} \theta r^2 \]

其中，θ为圆心角的弧度值，r为扇形的半径。这个公式体现了扇形面积与圆心角弧度值及半径平方之间的正比关系。当圆心角为2π（即整圆）时，扇形面积即为圆面积，验证了公式的正确性。

2. 基于圆心角的度数值

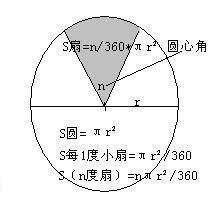
在实际应用中，圆心角有时也以度为单位给出。此时，扇形面积的计算需要先将圆心角的度数转换为弧度，但为了方便记忆与应用，也存在直接基于度数的公式变种，即先计算圆心角占整圆（360°）的比例，再乘以圆面积：

\[ S_{扇形} = \left( \frac{\theta^\circ}{360^\circ} \right) \times \pi r^2 \]

这里的θ°表示圆心角的度数。此公式虽然间接，但直接反映了扇形占整个圆面积的比例关系，便于理解。

3. 通过扇形弧长计算

除了直接利用圆心角和半径外，扇形面积还可以通过其弧长和半径来计算。扇形弧长公式为L = θr（θ为弧度值），结合圆面积与周长的关系，可以推导出扇形面积的另一个表达式：

\[ S_{扇形} = \frac{1}{2} \times L \times r \]

这里L是扇形的弧长，r为半径。此公式揭示了扇形面积与其弧长和半径之间的几何关系，提供了一种从弧长角度思考扇形面积的新视角。

三、公式应用与实例分析

应用实例一：基于弧度值

假设有一个扇形，其半径为5cm，圆心角为π/3弧度，求该扇形的面积。

\[ S_{扇形} = \frac{1}{2} \times \frac{\pi}{3} \times 5^2 = \frac{25\pi}{6} \text{cm}^2 \]

应用实例二：基于度数值

再假设另一个扇形，其半径同样为5cm，但圆心角为60°。此时，需先将角度转换为弧度或使用基于度数的公式：

使用转换法：\[ \theta = 60^\circ \times \frac{\pi}{180} = \frac{\pi}{3} \] 然后同上计算。

或直接使用基于度数的公式：\[ S_{扇形} = \left( \frac{60^\circ}{360^\circ} \right) \times \pi \times 5^2 = \frac{25\pi}{6} \text{cm}^2 \]

应用实例三：通过弧长计算

若某扇形弧长为5π/3cm，半径为5cm，求其面积。

\[ S_{扇形} = \frac{1}{2} \times \frac{5\pi}{3} \times 5 = \frac{25\pi}{6} \text{cm}^2 \]

四、结语

通过上述介绍，我们深入了解了扇形面积的三个核心计算公式，它们分别从圆心角的弧度值、度数值以及扇形弧长的角度出发，为我们提供了灵活多样的计算方法。掌握这些公式不仅能够帮助我们解决几何问题，还能培养我们对空间形状与数量关系的直觉感知。在未来的学习与研究中，扇形面积的计算将继续发挥其重要作用，成为连接基础与高阶几何知识的桥梁。